|
Консультант по электроснабжению
Не нашли нужный онлайн-расчет по электроэнергетике? Свяжитесь с нами!
Бот Яша
Бот Яша подскажет как найти нужный онлайн расчет или базу данных на сайте "Онлайн Электрик".
Написать боту.
Выбор типа модели асинхронного двигателя при компьютерном моделировании электромеханических процессов, протекающих в частотных электроприводах с алгоритмами скалярного и векторного управленияАлексеев В.В., Вершинин В.И., Козярук А.Е.Санкт-Петербургский государственный горный университет, Язев В.Н. Сибирский федеральный университет
В процессе проведения опытно-конструкторских работ по созданию регулируемых электроприводов (ЭП) различного назначения на определенных стадиях проектирования (эскизный проект, технический проект) требуется выбрать структуру разрабатываемого ЭП и алгоритмы его управления. В целях проверки правильности принимаемых решений на этих стадиях проектанты ЭП сегодня широко применяют методы компьютерного исследования электромеханических процессов, протекающих в моделях ЭП, позволяющие производить оценку соответствия динамических характеристик разрабатываемого ЭП требованиям, приведенным в техническом задании. Для решения задач подобного рода существуют различные компьютерные технологии, в основе которых лежат пакеты прикладных программ. Наиболее распространенным среди таковых является пакет MATLAB с различными дополнениями, из числа которых Toolbox Simulink, удобный при проведении анализа электромеханических процессов, протекающих в ЭП.
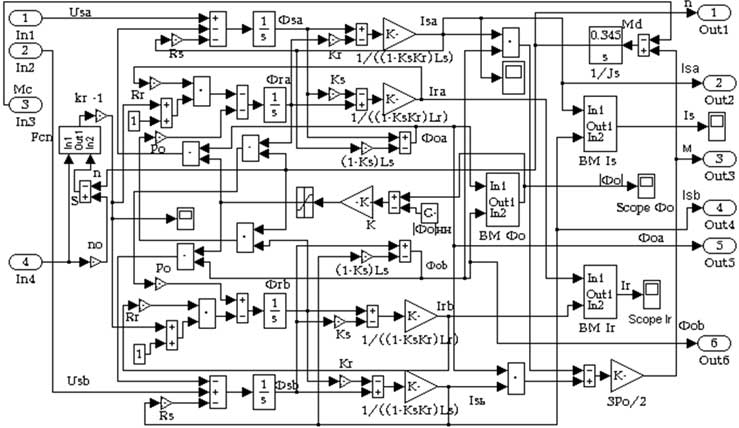
Основным достоинством этого дополнения является наличие библиотечных моделей, имитирующих практически все элементы, входящие в состав ЭП, в том числе и исполнительные двигатели. Модель асинхронного двигателя наиболее удобна при исследовании традиционной векторной системы с опорным вектором потокосцепления ротора Ψr типа Transvektor. В последних версиях можно ввести кривые намагничивания железа (ротора). В ряде версий MATLAB (Simulink) полностью раскрыть эти модели, а главное редактировать их не представляется возможным. При использовании библиотечной модели асинхронного двигателя (АД) с короткозамкнутым ротором не ясно, как учтен эффект вытеснения тока в роторе, который характерен для отечественных АД, например, серий 4А, 5А, АИР. Требуется оценка возможностей применения модели в других ЭП. Векторная система с опорным вектором главного потокосцепления Ψ0 (магнитной индукции в воздушном зазоре), рассматриваемая в данной статье, имеет ряд отличительных особенностей. Набор переменных состояния, включающий Ψ0 определяет структуру системы, с прямым управлением главным потокосцеплением, исключающую контур составляющей тока i1. Электропривод имеет отличные от системы Transvektor характеристики, в том числе энергетические, иную перегрузочную способность, исключает вход магнитной системы в глубокое насыщение, и делает ее привлекательной в ряде применений [1-4]. Однако измерение параметров вектора главного потокосцепления с помощью библиотечной модели (Demux) в пакете MATLAB не предусмотрено. Требуется дополнить модель вычислителем составляющих вектора Ψ0, что позволяет применить рациональный метод учета насыщения магнитной цепи в системе с опорным вектором Ψ0. Возможности пакета Toolbox Simulink позволяют проектанту создавать самостоятельно модели исполнительных двигателей, учитывающие дополнительные эффекты. Такая модель асинхронного двигателя строятся на основании системы уравнений Горева-Парка, записанных применительно к АД с короткозамкнутым ротором [2]. В этой модели АД рис.1 предусмотрен учет как насыщения, так эффекта вытеснения тока в роторе. Модель двухфазного асинхронного двигателя на рис.1 представлена в неподвижной системе координат с использованием составляющих потокосцеплений и токов в неподвижных осях α, β [5]. Процессы в двигателе описываются уравнениями равновесия напряжений и моментов, уравнениями токов статора и ротора: 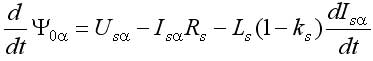 ; (1) ; (1)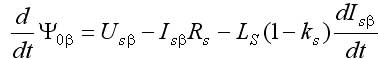 ; (2) ; (2)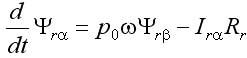 ; (3) ; (3)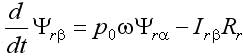 ; (4) ; (4)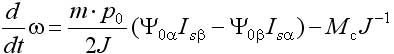 ; (5) ; (5)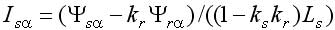 ; (6) ; (6)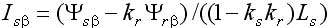 ; (7) ; (7)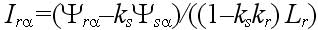 ; (8) ; (8)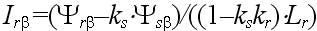 . (9) . (9)В формулах (1...9): Is, Ψ0, Ψs, Ψr, Us – проекции обобщенного вектора тока статора, главного потокосцепления, потокосцепления статора и ротора, напряжения статора на оси α, β; m – число фаз статора; ks – коэффициент магнитной связи статора; kr – коэффициент магнитной связи ротора; (1–kskr)Ls=L’s и (1–kskr)Lr=L’r – переходные индуктивности статора и ротора; J – момент инерции; p0 – число пар полюсов. В электрических машинах с относительно малым воздушным зазором, к которым относятся в асинхронные машины, насыщение в некоторых случаях необходимо учитывать при расчетах. Для этого можно ввести параметр γн, равный отношению магнитного потока насыщения к номинальному магнитному потоку |Ψ0| нн/| Ψ0|н. Введение нединамических нелинейностей в модель для учета насыщения, как известно, связано с принципиальными трудностями. Проблему можно решить, преобразовав уравнения (1), (2) и синтезировав правые части полученных уравнений, обеспечивающие получение жесткого предельного цикла при достижении главным потокосцеплением |Ψ0| уровня заданного насыщения |Ψ0| нн при |Ψ0|–|Ψ0| нн> 0, в соответствии с уравнениями [5]: 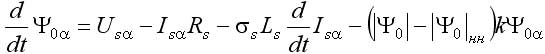 ; (10) ; (10)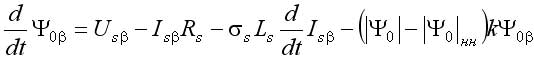 , (11) , (11)где |Ψ0| = (Ψ0α2+Ψ0β2)0,5 ≈Uф/(4,44·f) – модуль главного потокосцепления, Вб; k – коэффициент. Эффект вытеснения тока в роторе характеризуется изменением активного r’2 и реактивного сопротивления рассеяния x’2 ротора в наибольшей степени проявляется при прямом пуске АД. Без использования этого эффекта кратность пускового момента АД 4А (при P > 1 кВт) Кпм< 1. Для приближенного учета эффекта вытеснения, надо знать высоту стержня ротора. Например, у двигателя 4A280S6 высота стержня ротора h = 3,45 см. Эквивалентное увеличение активного сопротивления пазовой части алюминиевого стержня определяется коэффициентом Кr, который зависит от приведенной высоты стержня ξ, зависящей, в свою очередь, от скольжения s ξ ≈ 0,07h(ω1s) 0,5, (12) где s – скольжение; ω1 = ω/p0 = 314,1/3 = 104,7 рад/с. Коэффициентом Кr нелинейно зависит от высоты стержня. Приближенно при 0<ξ < 1, коэффициент Кr постоянен Кr0 = 1. Эффекта вытеснения нет (например, при прямом пуске s=1 и h < 1,4 см). При ξ > 1 Кr = Кr0 + ξ – 1 = ξ. Коэффициент снижения сопротивления x’2 К x ≈ 1,5/ Кr. Значение пускового момента при прямом пуске приближенно, с учетом увеличения активного сопротивления пазовой части стержня ротора, а также уменьшения индуктивного сопротивления от действия эффекта вытеснения, можно оценить по формуле 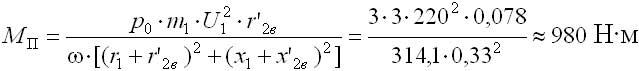 , ,Такой момент при прямом пуске двигателя 4A280S6 получается за счет увеличения r’2 с 0,031 до 0,078 Ом (рост Mп в 2,3 раза), и снижения x’2 с 0,194 до 0,118 Ом – (рост Мп в 1,46 раза). В уравнения модели АД (1-9) сопротивление x’2 явном виде не входит. Для двигателей 4А мощностью 11...400 кВт x1≈x’2; r1≈r’2; x1>5r1. Следовательно, приблизительно такое же суммарное увеличение момента при пуске получим К’r, увеличив коэффициент Кr в 4/(1+ Кx)2 раз, оставляя постоянным значение x’2. При этом принимается, что увеличение r’2 имеет наиболее существенное влияние на рост пускового момента, а учет только увеличения активного сопротивления пазовой части стержня ротора компенсируется влиянием на x’2 насыщения коронок зубцов. Это упрощает модель АД с учетом вытеснения тока. Уточненный расчет влияния эффекта вытеснения тока в роторе изложен в [6] и реализуется, например, в программе Mathcad. Эффект вытеснения проявляется при больших значениях скольжения. Например, для 4А280S6 при ω1 = 104,7 рад/с эффект проявляется при скольжении 0,16 (критическое скольжение АД 4A280S6 равно 0,07, а номинальное - 0,02). Формула (12) дает оценку значения ξ при ω1 = 104,7 рад/с, а, следовательно, при меньших ω1 ξ уменьшается пропорционально (ω1) 0,5. Очевидно, что для векторных систем и частично для скалярных систем эффект вытеснения практического значения не имеет. Это подтверждают результаты моделирования. Моделирование прямого пуска с учетом эффекта вытеснения (рис.1) дает время пуска для 4A280S6 из справочника для асинхронных двигателей серии 4A, а без учета эффекта вытеснения с моделью (АД из пакета MATLAB) время пуска tп0 оценивается с ошибкой более 100% [5]. В целях учета эффекта вытеснения тока в модели рис.1, проявляющегося при больших значениях скольжения s, используется сигнал пропорциональный синхронной скорости вращения n0. Для определения коэффициента вытеснения Кr’ после блока вычисления абсолютного скольжения S включен блок подсистемы Fcn, в который введено вычисляемое выражение [0,07h (sω1)0,5] – 1. Постоянная величина Кr0 = 1 введена на вход сумматора. Эффект насыщения магнитной цепи моделируется с помощью блока, в который вводится значение потока насыщения Ф0нн. Модель, схема которой приведена на рис.1, имеет параметры АД типа 4А280S6. Величины модулей главного потокосцепления и тока статора нужны при моделировании частотно-регулируемой системы со скалярным алгоритмом управления. В настоящей работе приводятся результаты исследований электромеханических процессов, протекающих в моделях частотно-регулируемых ЭП переменного тока с различными алгоритмами управления (скалярным и векторным), а также проводится сопоставительный анализ этих процессов. Исследуемые модели ЭП строились на основе двух видов моделей исполнительных двигателей: - библиотечная модель АД (Asynchronous Machine SI Units) из пакета MATLAB; - модель АД, построенная в соответствии с уравнениями Горева–Парка, учитывающими эффекты насыщения магнитной цепи и вытеснения тока.
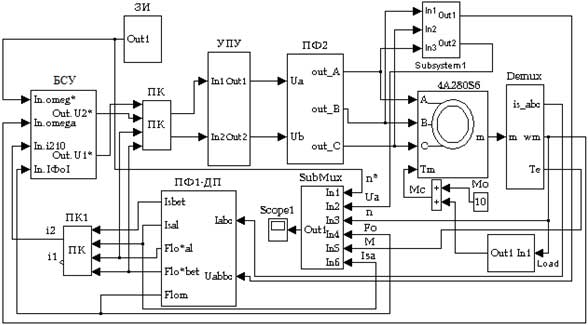
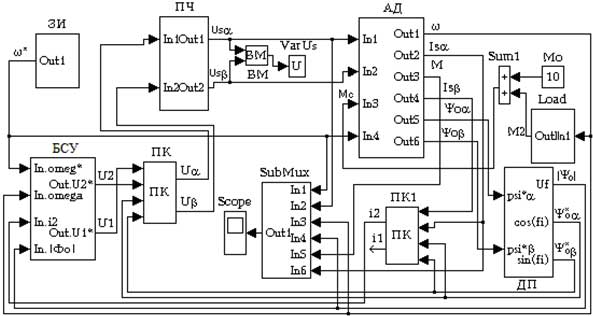
Указанные исследования проводились в целях выявления областей целесообразного применения различных типов моделей АД, используемых в процессе компьютерного моделирования электромеханических процессов, протекающих в частотно–регулируемых ЭП. Схемы исследуемых моделей частотно-регулируемых векторных ЭП с опорным вектором главного потокосцепления приведены на рис.2, рис.3. При этом модель ЭП, приведенная на рис.2, была построена на основе библиотечной модели АД. А схема модели, показанной на рис.3, построена с использованием модели АД, созданной на основе уравнений Горева–Парка (1-11), записанных в неподвижной относительно статора системе координат α, β.
Обе использованные модели АД, были построены с учетом параметров исполнительного двигателя типа 4А280S6, приведенных в таблице. При оценке сравнимости результатов учитывались следующие положения. 1. Модель двухфазной модели АД полностью отражает процессы в эквивалентной трехфазной машине. 2. Введение преобразователей фаз не вносит искажений в процессы. При этом преобразователь фаз ПФ2 (рис.2) настроен так, что вектор сигнала U&alpha равен вектору UA [2, 3]. 3. За основу взята система рис.3, имеющая минимум блоков, и в нее введены дополнительные необходимые блоки, с учетом особенностей библиотечной модели АД и векторной системы с опорным вектором главного потокосцепления. 4. В качестве библиотечной модели принята модель пакета MATLAB 6.5.
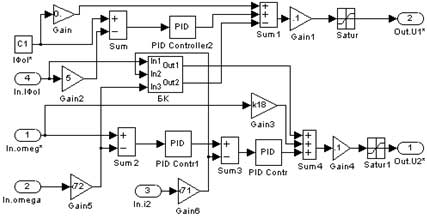
В обеих моделях используются идентичные блоки системы управления электроприводом БСУ, обеспечивающие управление работой АД по двум каналам: - канал поддержания постоянства магнитного потока; - канал управления электромагнитным моментом. Схема этого блока приведена на рис.4. Блок компенсации (БК) позволяет оценить влияние перекрестных связей каналов в реальном двигателе.
Диаграммы электромеханических процессов, протекающих в обеих компьютерных моделях частотно-регулируемых ЭП с алгоритмом векторного управления по вектору главного потокосцепления, приведены на рис.5, рис.6. На приведенных диаграммах показаны процессы изменения напряжения Us и тока Is статора, частоты вращения ω, электромагнитного момента и модуля вектора главного потокосцепления |Ψ0|, протекающие при пуске и равноускоренном разгоне АД до номинальной частоты вращения ( рад/c), набросе и сбросе статического момента нагрузки ( Нм), а также при равнозамедленном снижении частоты вращения АД до полной остановки. Сравнительный анализ приведенных диаграмм свидетельствует об их практически полной идентичности. Исходя из этого обстоятельства, можно заключить следующее. В процессе компьютерного моделирования электромеханических процессов, протекающих в частотно – регулируемых ЭП с алгоритмом векторного управления, с одинаковой степенью достоверности можно пользоваться как библиотечной моделью АД, так и его моделью, построенной на основе уравнений Горева–Парка, которые учитывают эффект насыщения магнитной цепи и эффект вытеснения тока ротора. Этот вывод объясняется тем, что в частотно–регулируемых ЭП с векторным управлением магнитная цепь двигателя не входит в режим насыщения, вследствие поддержания постоянства магнитного потока (индукции в воздушном зазоре машины). А эффект вытеснения тока ротора незначителен и практически не влияет на характер протекания электромеханических процессов, протекающих в электроприводе. 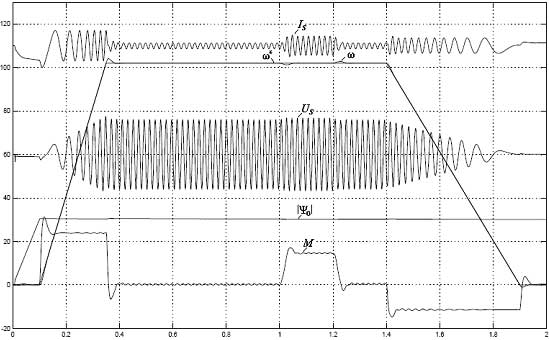 Рис.5. Диаграммы электромеханических процессов, протекающих в компьютерной модели ЭП с алгоритмом векторного управления по вектору главного потокосцепления, построенной на основе библиотечной модели АД 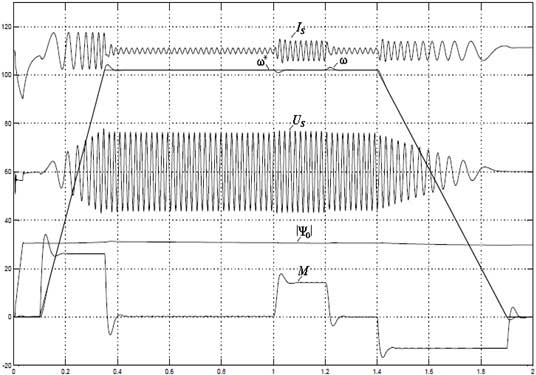 Рис.6. Диаграммы электромеханических процессов, протекающих в компьютерной модели частотно-регулируемого ЭП с алгоритмом векторного управления по вектору главного потокосцепления, построенной на основе модели АД по уравнениям Горева-Парка Аналогичные исследования были проведены применительно к компьютерным моделям частотно-регулируемого ЭП с алгоритмом скалярного управления, схемы которых приведены на рис.7, рис.8. В одной из них (рис.7) использовалась библиотечная модель АД, в другой - модель двигателя, построенная на основе уравнений Горева-Парка. Следует отметить, что как и векторной системе для использования библиотечной модели АД в блоке ПФ2 требуется введение дополнительных блоков Konnector и Controller Voltage Sourse. 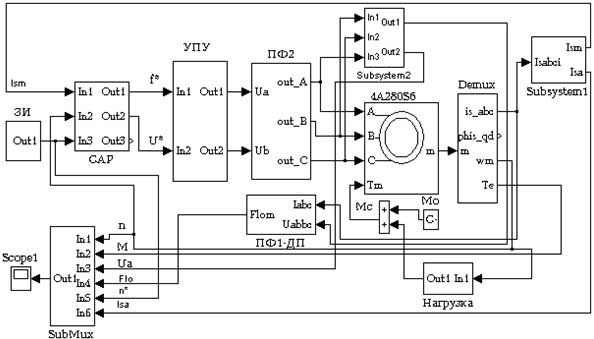 Рис.7. Схема модели частотно-регулируемого электропривода с алгоритмом скалярного управления, построенная на основе библиотечной модели АД 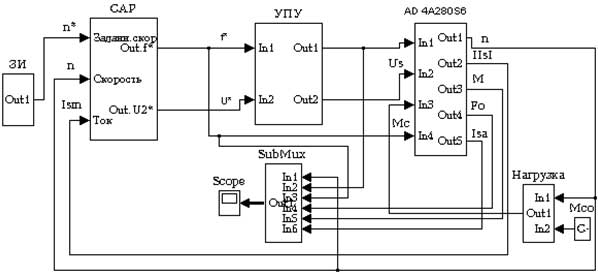 Рис.8. Схема модели частотно-регулируемого электропривода с алгоритмом скалярного управления, построенная на основе модели АД синтезированной по уравнениям Горева-Парка Диаграммы электромеханических процессов, протекающих в этих компьютерных моделях, приведены на рис.9, рис.10. 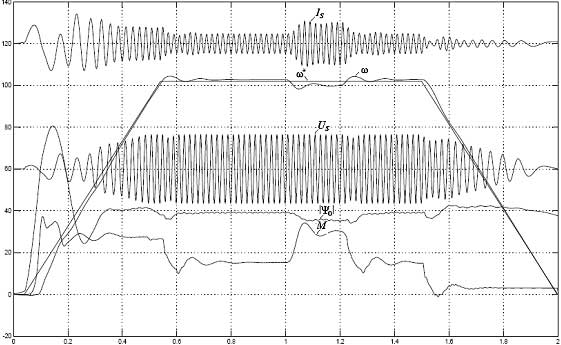 Рис.9. Диаграммы электромеханических процессов, протекающих в компьютерной модели частотно-регулируемого ЭП с алгоритмом скалярного управления, построенной на основе библиотечной модели АД 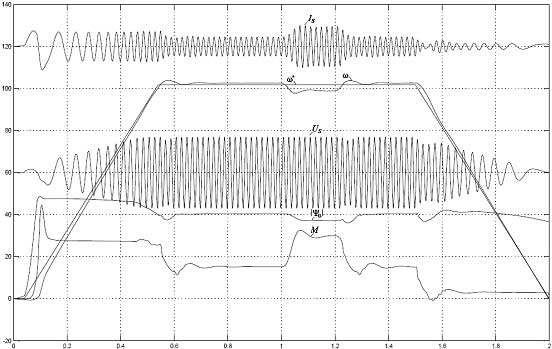 Рис.10. Диаграммы электромеханических процессов, протекающих в компьютерной модели частотно-регулируемого ЭП с алгоритмом скалярного управления, построенной на основе модели АД, синтезированной по уравнениям Горева-Парка В результате анализа приведенных диаграмм можно отметить следующее. Если принять, что модель ЭП, в которой учитываются эффект насыщения магнитной цепи АД и эффект вытеснения тока ротора адекватно описывает протекание электромеханических процессов в реальном ЭП, то тогда можно заключить, что оценка электромеханических процессов, протекающих в ЭП на основе библиотечной модели АД MATLAB 6.5 будет иметь существенную погрешность. Причем эта погрешность в большей степени характерна для описания динамических процессов при прямом пуске АД и в скалярных системах. В частности, относительные погрешности в оценке величины модуля вектора магнитного потока, тока статора, электромагнитного момента, при пуске и разгоне АД составляют 77, 100 и 18% соответственно. Для оценки применимости библиотечной модели, снабженной кривыми намагничивания, требуются дополнительные исследования в части применимости в векторной системе с опорным вектором главного потокосцепления. Выводы. 1. При проведении компьютерных исследований электромеханических процессов, протекающих в частотно-регулируемых электроприводах с алгоритмом векторного управления, использование библиотечной модели АД из дополнения Toolbox Simulink к пакету прикладных программ MATLAB является вполне допустимым и оправданным при введении дополнительных блоков для реализации управления по вектору главного потокосцепления Ψ0 и стабилизации модуля |Ψ0|. 2. При проведении компьютерных исследований электромеханических процессов, протекающих в приводах с прямым пуском АД и частотно-регулируемых электроприводах с алгоритмом скалярного управления, при пуске с высоким темпом (T> 103 рад/с2 для АД 4A280S6, рис.8) целесообразным является использование модели АД, построенной на основе уравнений Горева–Парка, учитывающей эффекты насыщения магнитной цепи и вытеснения тока ротора исполнительного двигателя, и, как следствие этого, обеспечивающую большую точность моделирования переходных режимов, характеризующихся значительным скольжением. 1. Теоретические основы построения частотных электроприводов с векторным управлением / В.А.Дартау, В.В.Рудаков, А.Е.Козярук, Ю.П.Павлов, А.Л.Аверкиев //Автоматизированный электропривод. М.: Энергия, 1980, С. 93-101. 2. Рудаков В.В., Столяров И.М., Дартау В.А. Асинхронные электроприводы с векторным управлением. - Л.: Энергоатомиздат, 1987, 136 с. 3. Выбор системы координат при реализации алгоритма векторного управления асинхронным электроприводом/Алексеев В.В., Козярук А.Е., Рудаков, Язев В.Н.// Электротехника. 2010. №12, С. 2-9. 4. Дартау В.А. Переходные процессы в электрических машинах переменного тока с насыщением / Записки ЛГИ. Т.128, СПб, 1991, С. 52- 57. 5. Алексеев В.В., Загривный Э.А., Козярук А.Е. Электрические машины. Моделирование электрических машин приводов горного оборудования. СПб. СПГГИ., 2006, 58 с. 6. Проектирование электрических машин/И.П. Копылов, Ф.А. Горяинов, Б.К. Клоков, В.П. Морозкин, Б.Ф. Токарев; Под ред. И.П. Копылова. М.: Энергия, 1980. 496 с. Библиографическая ссылка на статью: Алексеев В.В., Вершинин В.И., Козярук А.Е., Язев В.Н. Выбор типа модели асинхронного двигателя при компьютерном моделировании электромеханических процессов, протекающих в частотных электроприводах с алгоритмами скалярного и векторного управления // Онлайн Электрик: Электроэнергетика. Новые технологии, 2012.–URL: /articles.php?id=11 (Дата обращения: 18.02.2026)
|